Équations de Lotka-Volterra
En mathématiques, les équations de Lotka-Volterra, qu'on désigne aussi sous le terme de "modèle proie-prédateur", sont un couple d'équations différentielles non-linéaires du premier ordre,...
Pages similaires :
- Quand la population de prédateur a suffisamment diminué, les proies profitant... Le contenu de cette page (Équations de Lotka-Volterra) est un minuscule... (source : books.google)
En mathématiques, les équations de Lotka-Volterra, qu'on désigne aussi sous le terme de "modèle proie-prédateur", sont un couple d'équations différentielles non-linéaires du premier ordre, et sont couramment utilisées pour décrire la dynamique de systèmes biologiques dans lesquels un prédateur et sa proie interagissent. Elles ont été proposées indépendamment par Alfred J. Lotka en 1925 et Vito Volterra en 1926. Ce système d'équations est classiquement utilisé comme modèle pour la dynamique du lynx et du lièvre des neiges, pour laquelle de nombreuses données de terrain ont été collectées sur les populations des deux espèces par la Compagnie de la baie d'Hudson au XIXe siècle.
Les équations
Elles s'écrivent souvent :
où
- x (t) est l'effectif des proies;
- y (t) est l'effectif des prédateurs;
- t est le temps;
- dx (t) / dt et dy (t) / dy représentent les taux de croissance des populations au cours du temps;
- α, β, γ et δ sont des paramètres caractérisant les interactions entre les deux espèces.
Signification physique des équations
Une fois développées, les équations prennent une forme utile pour une interprétation physique.
Proies
L'équation de la proie devient :
Les proies sont supposées avoir une source infinie de nourriture et se reproduire exponentiellement s'ils ne sont soumis à aucune prédation ; cette croissance exponentielle est représentée dans l'équation ci-dessus par le terme αx (t) . Le taux de prédation sur les proies est supposé proportionnel à la fréquence de rencontre entre les prédateurs et les proies ; il est représenté ci-dessus par βx (t) y (t) . Si l'un des termes x (t) ou y (t) est nul, dans ce cas il ne peut y avoir aucune prédation.
Avec ces deux termes, l'équation peut dans ce cas être interprétée comme : la variation du nombre de proies est donnée par sa propre croissance moins le taux de prédation qui leur est appliqué.
Prédateurs
L'équation du prédateur devient :
Dans cette équation, δx (t) y (t) représente la croissance de la population prédatrice. (Notons la similarité avec le taux de prédation ; toutefois, une constante différente est utilisée car la vitesse à laquelle la population des prédateurs augmente n'est pas forcément égale à celle à laquelle il consomme la proie). De plus, γy (t) représente la mort naturelle des prédateurs ; c'est une décroissance exponentielle. L'équation représente par conséquent la variation de la population de prédateurs comme croissance de cette population, diminuée du nombre de morts naturelles.
Solutions de l'équation
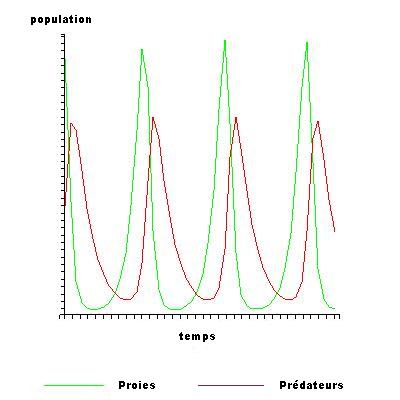
Les équations admettent des solutions périodiques qui n'ont pas d'expressions simple avec fonctions trigonométriques habituelles. Néanmoins, une solution approximative linéarisée offre un mouvement harmonique simple, avec la population des prédateurs en retard de 90° (un quart de période) sur celle des proies.
Dynamique du système
Dans le modèle utilisé, les prédateurs prospèrent quand les proies sont nombreuses, mais finissent par épuiser leurs ressources et déclinent. Quand la population de prédateur a suffisamment diminué, les proies profitant du répit se reproduisent et leur population augmente de nouveau. Cette dynamique se poursuit en un cycle de croissance et déclin.
Equilibres de la population
Un état d'équilibre de la population est observé lorsque aucune des deux populations en présence n'évolue, c'est-à-dire lorsque les dérivées correspondantes sont nulles, ce qui se traduit par le système d'équations :
qui a pour solutions :
La première solution correspond à une extinction définitive des deux espèces, la deuxième à des valeurs pour les deux populations, dépendant des quatre paramètres α, β, γ et δ, qui restent stables indéfiniment.
Stabilité des points fixes
La stabilité des points fixes peut être déterminée par une linéarisation du système aux dérivées partielles. La matrice jacobienne du système est
En le premier point fixe (0,0) , cette matrice prend la valeur :
qui a pour valeurs propres :
Ces valeurs propres sont systématiquement de signes opposés, ce qui montre que ce point fixe est un point selle. Ce n'est par conséquent pas un point fixe stable, ce qui montre surtout que, suivant ce modèle, l'extinction des deux espèces en jeu est difficile à obtenir.
Second point fixe
En évaluant la matrice jacobienne en le second point fixe, la valeur suivante est obtenue :
et elle a pour valeurs propres :
Ce point fixe est par conséquent un foyer et plus particulièrement un centre, ce qui veut dire que les populations de proies et prédateurs oscillent autour de leurs valeurs en ce point fixe.
Voir aussi
Bibliographie
- E. R. Leigh (1968) The ecological role of Volterra's equations, in Some Mathematical Problems in Biology - a modern discussion using Hudson's Bay Company data on lynx and hares in Canada from 1847 to 1903.
- Understanding Nonlinear Dynamics. Daniel Kaplan et Leon Glass.
- V. Volterra. Variations and fluctuations of the number of individuals in animal species living together. In Animal Ecology. McGraw-Hill, 1931. Traduit de l'édition de 1928 par R. N. Chapman.
Liens externes
- Lotka-Volterra Predator-Prey Model by Elmer G. Wiens
- Modèle de Lotka-Volterra
Recherche sur Google Images : |
|
"Les équations admettent des ..." L'image ci-contre est extraite du site fr.wikipedia.org Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur. Voir l'image en taille réelle (400 x 400 - 18 ko - )Refaire la recherche sur Google Images |
Recherche sur Amazone (livres) : Refaire la recherche Refaire la recherche |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/11/2008.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.
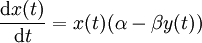
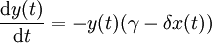
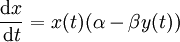
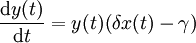
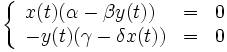
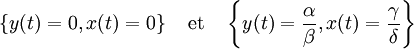
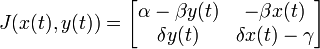
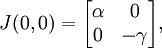
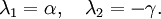
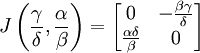
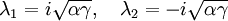

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité